Engineered Wood Beam Analysis: Shear and Moment Diagrams Explained

[jar546]

If you have any corrections or disputes, please comment below.

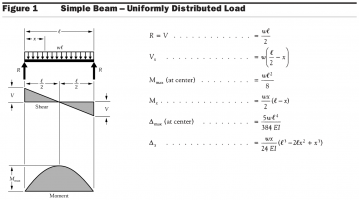
Figure 1 from the document titled "Beam Design Formulas with Shear and Moment Diagrams" presents a simple beam subjected to a uniformly distributed load. This figure is foundational for understanding the behavior of beams under distributed loads, which are common in many structural applications. Here's a breakdown of the key components and calculations provided in Figure 1 for a simple beam with a uniformly distributed load:

Description of the Beam and Load​

• The beam is depicted as a straight, horizontal member supported at both ends, indicating a simple or supported beam configuration.
• The load is uniformly distributed across the entire length of the beam, denoted by "w" (in lbs./in. or kN/m), representing the load per unit length.

Shear Force Diagram (V)​

• The shear force diagram shows how the shear force (V) varies along the length of the beam.
• At the supports, the shear force is equal to half the total applied load, indicating that the reactions at the supports are equal and balance the applied load.
• The shear force linearly decreases to zero at the midpoint of the beam. This linear variation is due to the uniform distribution of the load across the beam length.
• The shape of the shear force diagram is triangular, highlighting the linear change in shear force from the supports towards the center.

Moment Diagram (M)​

• The moment diagram illustrates the bending moment (M) experienced by the beam at any point along its length.
• The bending moment is maximum at the midpoint of the beam and zero at the ends (supports). This pattern reflects the beam's tendency to bend under the distributed load, with the maximum bending occurring at the center where the shear force is zero.
• The maximum bending moment (M_max) can be calculated using the provided formula, which is based on the load per unit length (w), and the span length of the beam (L).
• The shape of the moment diagram is parabolic, indicating that the bending moment varies nonlinearly along the length of the beam, reaching its peak at the center.

Key Formulas​

• The document provides formulas to calculate the reaction forces at the supports (R), the shear force (V) at any point along the beam, and the maximum bending moment (M_max). These calculations are crucial for designing the beam to ensure it can safely support the applied loads without failure.

Educational Significance​

Understanding Figure 1 and its implications is critical for engineers and designers, as it lays the groundwork for analyzing and designing beams subjected to uniformly distributed loads. The ability to interpret the shear and moment diagrams and use the associated formulas for calculating key structural parameters is fundamental in structural engineering, ensuring that designs are efficient and compliant with safety standards.

 

[Yankee Chronicler]

Simple beams are ... well, simple. What it comes down to in the end, which is of primary importance to code officials and inspectors, is that shear is greatest at the end supports and reduces to zero at mid-span, while bending moment is zero at the end supports and increases to a maximum at mid-span. We don't have to know how to calculate the exact numbers to understand how the structure works.

Once we see how the two diagrams illustrate that, it helps us to understand the diagrams for other loading conditions, such as

• Point load at mid-span
• Point load not at mid-span
• Concentrated load on partial span

These are sometimes not intuitive. Where there are multiple loading conditions (perhaps a uniform live load plus a point load at mid-span), the numbers can be computed independently and then added together to arrive at the overall loading diagram for the member.